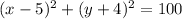Question

A circle is centered at the point (5, -4) and passes through the point (-3, 2). The equation of this circle is (x + )2 + (y + )2 = . Reset

Answer 1

`(x-5)^(2)+(y+4)^(2)=100`

Step-by-step explanation:

We have been given the center of the circle as (5, -4) and a point on the circumference as (-3, 2). We first determine the radius of the circle. The radius is the distance from the center to any point on the circumference. Using the distance formula, we have;

`radius=\sqrt{(5--3)^(2)+(-4-2)^(2)}\\radius=√(64+36)=10`

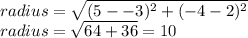
The radius of the circle is thus 10 units.

The equation of a circle with center (a,b) and radius r units is given as;

`(x-a)^(2)+(y-b)^(2)=r^(2)`

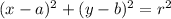
Plugging in the values given we have;

`(x-5)^(2)+(y+4)^(2)=100`