Answer:
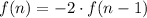 , where f(1)=3
, where f(1)=3
Explanation:
The given sequence is; 3, –6, 12, –24, 48, …
The first term of this sequence is
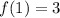
There is a common ratio of
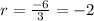
We can actually use any other two consecutive terms in the sequence to obtain the common ratio.
The recursive formula is given by:
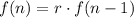
We plug in the common ratio to get:
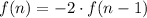 , where f(1)=3
, where f(1)=3