Question

Which recursive formula can be used to generate the sequence below, where f(1) = 3 and n ≥ 1?

3, –6, 12, –24, 48, …

f (n + 1) = –3 f(n )
f (n + 1) = 3 f(n )
f (n + 1) = –2 f(n )
f (n + 1) = 2 f(n)

Answer 1

The answer is C

Explanation:

Answer 2

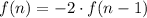`f(n)=-2\cdot f(n-1)`, where f(1)=3

Explanation:

The given sequence is; 3, –6, 12, –24, 48, …

The first term of this sequence is

`f(1)=3`

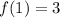
There is a common ratio of
`r=(-6)/(3)=-2`

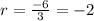
We can actually use any other two consecutive terms in the sequence to obtain the common ratio.

The recursive formula is given by:

`f(n)=r\cdot f(n-1)`

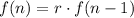
We plug in the common ratio to get:

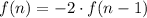`f(n)=-2\cdot f(n-1)`, where f(1)=3