Answer:
All events are independent
Explanation:
You are given the table
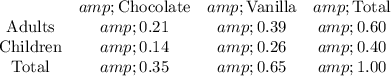
Two events A and B are independent when
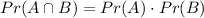
a) A="Chocolate"
B="Adults"
A and B="Chocolate and Adults"

Since
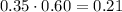 events are independent
events are independent
b) A="Children"
B="Chocolate"
A and B="Children and Chocolate"
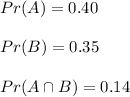
Since
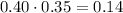 events are independent
events are independent
c) A="Vanilla"
B="Children"
A and B="Vanilla and Children"
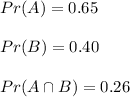
Since
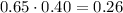 events are independent
events are independent