Answer:
# m∠A = 65.3°
# m∠A = 25.8°
# m∠A = 22.7°
Explanation:
* Lets revise the trigonometry function to solve the problem
- In any right angle triangle:
# The side opposite to the right angle is called the hypotenuse
# The other two sides are called the legs of the right angle
* If the name of the triangle is ABC, where B is the right angle
∴ The hypotenuse is AC
∴ AB and BC are the legs of the right angle
- ∠A and ∠C are two acute angles
- For angle A
# sin(A) = opposite/hypotenuse
∵ The opposite to ∠A is BC
∵ The hypotenuse is AC
∴ sin(A) = BC/AC
# cos(A) = adjacent/hypotenuse
∵ The adjacent to ∠A is AB
∵ The hypotenuse is AC
∴ cos(A) = AB/AC
# tan(A) = opposite/adjacent
∵ The opposite to ∠A is BC
∵ The adjacent to ∠A is AB
∴ tan(A) = BC/AB
* Lets solve the problems
# In Δ ABC
∵ m∠B = 90°
∵ AB = 2.3 ⇒ adjacent to angle A
∵ BC = 5 ⇒ apposite to angle A
- To find m∠A use the tangent function because we have opposite
and adjacent sides
∴ tan A = BC/AB
∴ tan A = 5/2.3 ⇒ use tan^-1 to find m∠A
∴ m∠A =
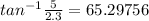
* m∠A = 65.3°
# In Δ ABD
∵ m∠B = 90°
∵ AB = 5.4 ⇒ adjacent to angle A
∵ DA = 6 ⇒ the hypotenuse
- To find m∠A use the cosine function because we have adjacent
and hypotenuse sides
∴ cos A = AB/DA
∴ cos A = 5.4/6 ⇒ use cos^-1 to find m∠A
∴ m∠A =
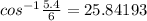
* m∠A = 25.8°
# In Δ ABE
∵ m∠B = 90°
∵ EB = 2.4 ⇒ opposite to angle A
∵ EA = 6.8 ⇒ the hypotenuse
- To find m∠A use the sine function because we have opposite
and hypotenuse sides
∴ sin A = EB/EA
∴ sin A = 2.4/6.8 ⇒ use sin^-1 to find m∠A
∴ m∠A =
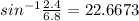
* m∠A = 22.7°