1. Filling in the table is just a matter of plugging in the given
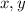 values into the ODE
values into the ODE
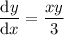 :
:

2. I've attached what the slope field should look like. Basically, sketch a line of slope equal to the value of
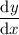 at the labeled point (these values are listed in the table).
at the labeled point (these values are listed in the table).
3. This ODE is separable. We have
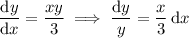
Integrating both sides gives
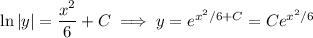
With the initial condition
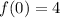 , we take
, we take
 and
and
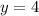 to solve for
to solve for
 :
:

Then the particular solution is

4. First, solve the ODE (also separable):
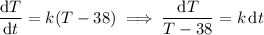
Integrating both sides gives

Given that
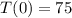 , we can solve for
, we can solve for
 :
:
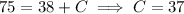
Then use the other condition,
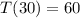 , to solve for
, to solve for
 :
:

Then the particular solution is

Now, you want to know the temperature after an additional 30 minutes, i.e. 60 minutes after having placed the lemonade in the fridge. According to the particular solution, We have
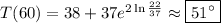
5. You want to find
 such that
such that
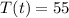 :
:

