Answer:
The given function is odd
Explanation:
we need to determine the function
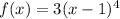 is odd or even
is odd or even
Since, A function f(x) is said to be even if
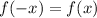
and f(x) is said to be odd if
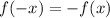 and
and
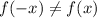
We Replace x with -x in the given function and solve;
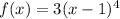
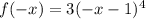
take out the negative common,
![f(-x)=3[-(x+1)]^(4)](https://img.qammunity.org/2020/formulas/mathematics/high-school/zcy459gi0vw6akqd4phpweql5sr5ly5vea.png)
Since
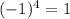
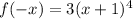
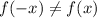
Hence, the given function is odd