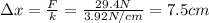Question

A 10-cm-long spring is attached to the ceiling. When a 2.0 kg mass is hung from it, the spring stretches to a length of 15 cm. How long when a 3.0 kg mass is suspended from it?

Answer 1

7.5 cm

Step-by-step explanation:

The force exerted by the 2.0 kg on the spring is equal to the weight of the mass, so:

`F=mg = (2.0 kg )(9.8 m/s^2)=19.6 N`

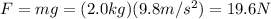
And this force causes a stretching of:

`\Delta x = 15 cm - 10 cm = 5 cm`

So we can use Hooke's law:

`F=k \Delta x`

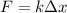
to find k, the spring constant:

`k=(F)/(\Delta x)=(19.6 N)/(5 cm)=3.92 N/cm`

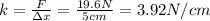
Now a new mass of m = 3.0 kg is attached to the spring; the force applied by this mass is

`F=mg=(3.0 kg)(9.8 m/s^2)=29.4 N`

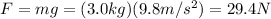
So we can use again Hooke's law to find the new stretching:

`\Delta x = (F)/(k)=(29.4 N)/(3.92 N/cm)=7.5 cm`