Question

Simplify the expression 3x3^ 648x 4 y8

Answer 1

Answer: B.) 18x^2y^2 3squareroot 3xy^2

Explanation:

Answer 2

B.
`18x^(2) y^(2) \sqrt[3]{3xy^(2) }`

Explanation:

To simplify this expression, use the fact that the root of a number (in this case is the cube root) can be expressed like a fractional exponent (1/3). Using this, the expression changes to:

`3x(648x^(4)y^(8))^((1/3))`

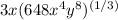
Next step is to put the exponent inside the parenthesis:

`3x(648^(1/3)x^(4/3)y^(8/3))`

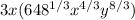
Find the prime factorization of 648:

648 =3⋅3⋅3⋅3⋅2⋅2⋅2

648=3⁴∗2³

`3x(3^((4/3))2^((3/3))x^(4/3)y^(8/3))`

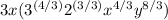
Change all improper fractions in exponent to mixed fractions

`3x(3^(1(1/3))2^(1)x^(1(1/3))y^(2(2/3)))`

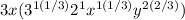
Separate integers exponents from fractional:

`3x(3\cdot3^((1/3))\cdot 2 \cdot x\cdot x^(1/3)\cdot y^(2)\cdot y^(2/3))`

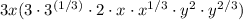
Re-arrange (all numbers with fractional exponents must be together):

`3x(3 \cdot 2\cdot x\cdot y^(2)\cdot 3^((1/3))x^(1/3)y^(2/3))`

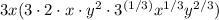
Multiply the 3x with the numbers that have an integer exponent:

`18x^(2)y^(2)(3^((1/3))x^(1/3)y^(2/3))`

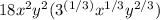
Take out the exponent 1/3 from the parenthesis:

`18x^(2)y^(2)(3xy^(2))^(1/3)`

And change the representation of the root to use a radical symbol

`18x^(2) y^(2) \sqrt[3]{3xy^(2) }`