Question

Which shows the correct substitution of the values a, b, and c from the equation 0 = – 3x2 – 2x + 6 into the quadratic formula? Quadratic formula: x =

Answer 1

`x=(-(-2)\pm √((-2)^2-4(-3)(6)))/(2(-3))`

Explanation:

The given quadratic equation is

`-3x^2-2x+6=0` .... (1)

If a quadratic equation is defined as

`ax^2+bx+c=0` .... (2)

then the quadratic formula is

`x=(-b\pm √(b^2-4ac))/(2a)`

On comparing (1) and (2), we get

`a=-3,b=-2,c=6`

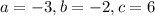
Substitute
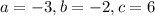`a=-3,b=-2,c=6` in the above formula.

`x=(-(-2)\pm √((-2)^2-4(-3)(6)))/(2(-3))`

Therefore, the correct substitution of the values a, b, and c in the quadratic formula is
`x=(-(-2)\pm √((-2)^2-4(-3)(6)))/(2(-3))`.

Answer 2

The answer in the procedure

Explanation:

we know that

The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`0=-3x^(2) -2x+6`

so

`a=-3\\b=-2\\c=6`

substitute in the formula

`x=\frac{-(-2)(+/-)\sqrt{-2^(2)-4(-3)(6)}} {2(-3)}`

`x=\frac{2(+/-)√(74)} {-6}`

`x=\frac{-2-√(74)} {6}`

`x=\frac{-2+√(74)} {6}`