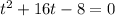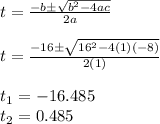Answer:
-IF THE EQUATION IS
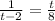 , THEN:
, THEN:
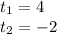
-IF THE EQUATION IS
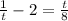 , THEN:
, THEN:
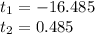
Explanation:
-IF THE EQUATION IS
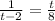 THE PROCEDURE IS:
THE PROCEDURE IS:
Multiply both sides of the equation by
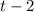 and by 8:
and by 8:
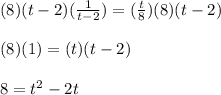
Subtract 8 from both sides of the equation:
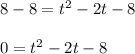
Factor the equation. Find two numbers whose sum be -2 and whose product be -8. These are -4 and 2:
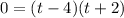
Then:
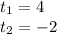
-IF THE EQUATION IS
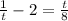 THE PROCEDURE IS:
THE PROCEDURE IS:
Subtract
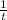 and
and
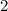 :
:
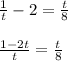
Multiply both sides of the equation by
 :
:
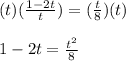
Multiply both sides of the equation by 8:
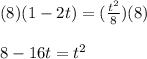
Move the
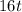 and 8 to the other side of the equation and apply the Quadratic formula. Then:
and 8 to the other side of the equation and apply the Quadratic formula. Then: