ANSWER
The two lines are perpendicular if
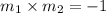
EXPLANATION
Given two lines:
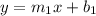
and
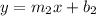
We can tell wether these two lines are perpendicular to each other using their slopes.
If the product of their slopes is -1, the then the two line are perpendicular.
For example:
The line
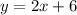
has slope
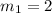
and the line
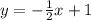
has slope
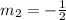
The product of the two slopes is
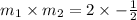
This implies that:
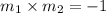
Therefore the two lines are perpendicular.