For this case we must find the point that Harold used to arrive at the following equation:
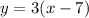
Starting from the fact that the equation of the point-slope form of a line is given by:

If we compare the standard equation with Harold's, we see that the slope of the line is
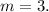
In addition, it is observed that
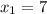 and
and
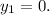
Then, the correct option is: Harold used the point (7,0)
ANswer:
When Harold wrote his equation, the point was used (7,0).