Question

What is the following product? Assume x ≥ 0

\sqrt[3]{x^{2} } . \sqrt[4]{x^{3} }


A. x\sqrt{x}

B. \sqrt[12]{x^{5} }

C. x(\sqrt[12]{x^{5} } )

D. x6

Answer 1

its c

Explanation:

Answer 2

For this case we must multiply the following expression:

`\sqrt [3] {x ^ 2} * \sqrt [4] {x ^ 3}`

By definition of properties of otencias and roots we have:

`\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}`

We rewrite the terms of the expression:

`\sqrt [3] {x ^ 2} = (x ^ 2) ^ {\frac {1} {3}} = (x ^ 2) ^ {\frac {4} {12}}\\\sqrt [4] {x ^ 3} = (x ^ 3) ^ {\frac {1} {4}} = (x ^ 3) ^ {\frac {3} {12}}`

So, we have:

`(x ^ 2) ^ {\frac {4} {12}} * (x ^ 3) ^ {\frac {3} {12}} =`

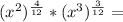
Applying the above definition we have:

`\sqrt [12] {(x ^ 2) ^ 4} * \sqrt [12] {(x ^ 3) ^ 3} =`

We multiply the exponents:

`\sqrt [12] {x ^ 8} * \sqrt [12] {x ^ 9} =`

We combine using the product rule for radicals.

`\sqrt [12] {x ^ 8 * x ^ 9} =`

By definition of multiplication properties of powers of the same base, we put the same base and add the exponents:

`\sqrt [12] {x ^ {8 + 9}} =\\\sqrt [12] {x ^ {17}} =\\\sqrt [12] {x ^ {12} * x ^ 5} =\\x \sqrt [12] {x ^ 5}`

Answer:

Option C