For this case we must multiply the following expression:
![\sqrt [3] {x ^ 2} * \sqrt [4] {x ^ 3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tik2pk0wg8zq0t2n131zdhgci910zq7edc.png)
By definition of properties of otencias and roots we have:
![\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/suo6ai2uezolc3t7f2f9e9h1lijquf271f.png)
We rewrite the terms of the expression:
![\sqrt [3] {x ^ 2} = (x ^ 2) ^ {\frac {1} {3}} = (x ^ 2) ^ {\frac {4} {12}}\\\sqrt [4] {x ^ 3} = (x ^ 3) ^ {\frac {1} {4}} = (x ^ 3) ^ {\frac {3} {12}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n92yl2eygm7rabxau6drm098we4xxkrlgz.png)
So, we have:
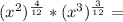
Applying the above definition we have:
![\sqrt [12] {(x ^ 2) ^ 4} * \sqrt [12] {(x ^ 3) ^ 3} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/m05kwlrg9umcqth7q146w0px959ixfvta3.png)
We multiply the exponents:
![\sqrt [12] {x ^ 8} * \sqrt [12] {x ^ 9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pqe7zapvbyju8o6ual66h1yppz3z37tgqh.png)
We combine using the product rule for radicals.
![\sqrt [12] {x ^ 8 * x ^ 9} =](https://img.qammunity.org/2020/formulas/mathematics/middle-school/erb8y10q6z97pvade0k6w8pw8dfln7o4tz.png)
By definition of multiplication properties of powers of the same base, we put the same base and add the exponents:
![\sqrt [12] {x ^ {8 + 9}} =\\\sqrt [12] {x ^ {17}} =\\\sqrt [12] {x ^ {12} * x ^ 5} =\\x \sqrt [12] {x ^ 5}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/d4ntneqbb7bqv34gqv5sf4soj3rc3y1hin.png)
Answer:
Option C