Answer:
155.80rad/s
Step-by-step explanation:
Using the equation of motion to find the angular acceleration:
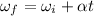
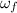 is the final angular velocity in rad/s
is the final angular velocity in rad/s
 is the initial angular velocity in rad/s
is the initial angular velocity in rad/s
 is the angular acceleration
is the angular acceleration
t is the time taken
Given the following
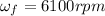
Time = 4.1secs
Convert the angular velocity to rad/s
1rpm = 0.10472rad/s
6100rpm = x
x = 6100 * 0.10472
x = 638.792rad/s
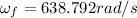
Get the angular acceleration:
Recall that:
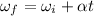
638.792 = 0 + ∝(4.1)
4.1∝ = 638.792
∝ = 638.792/4.1
∝ = 155.80rad/s
Hence the angular acceleration as the blades slow down is 155.80rad/s