Question

A pitcher claims he can throw a 0.146-kg baseball with as much momentum as a 2.70-g bullet moving with a speed of 1.50 ✕ 103 m/s. (a) What must the baseball's speed be if the pitcher's claim is valid? (b) Which has greater kinetic energy, the ball or the bullet? a. The bullet has greater kinetic energy. b. The ball has greater kinetic energy. c. Both have the same kinetic energy.

Answer 1

(a) The pitcher must throw the ball at 27.7 m/s

The momentum of an object is given by:

`p=mv`

where

m is the mass of the object

v is the object's velocity

Let's calculate the momentum of the bullet, which has a mass of

m = 2.70 g = 0.0027 kg

and a velocity of

`v=1.50\cdot 10^3 m/s`

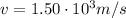
Its momentum is:

`p=mv=(0.0027 kg)(1.50\cdot 10^(3) m/s)=4.05 kg m/s`

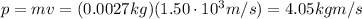
The pitcher must throw the baseball with this same momentum. The mass of the ball is

m = 0.146 kg

So the velocity of the ball must be

`v=(p)/(m)=(4.05 kg m/s)/(0.146 kg)=27.7 m/s`

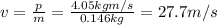
So, the pitcher must throw the ball at 27.7 m/s.

(b) a. The bullet has greater kinetic energy

The kinetic energy of an object is given by

`K=(1)/(2)mv^2`

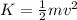
where m is the mass of the object and v is its speed.

For the bullet, we have:

`K=(1)/(2)(0.0027 kg)(1.50\cdot 10^3 m/s)^2=3037.5 J`

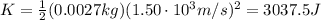
For the ball:

`K=(1)/(2)(0.146 kg)(27.7 m/s)^2=56.0 J`

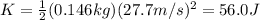
So, the bullet has greater kinetic energy.