Answer:

Explanation:
The length of the base is the distance between the points 4+2i and 10+4i, so
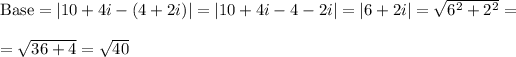
The middle point of the base is placed at point
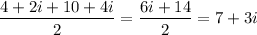
The length of the height is the distance between the points 5+9i and 7+3i
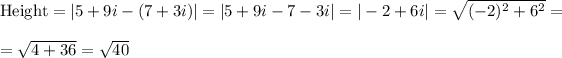
So, the area of the triangle is
