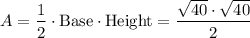Question

An isosceles triangle’s altitude will bisect its base. Which expression could be used to find the area of the isosceles triangle above?

Answer 1

A

Explanation:

did on edge

Answer 2

`(√(40)\cdot √(40))/(2)`

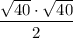
Explanation:

The length of the base is the distance between the points 4+2i and 10+4i, so

`\text{Base}=|10+4i-(4+2i)|=|10+4i-4-2i|=|6+2i|=√(6^2+2^2)=\\ \\=√(36+4)=√(40)`

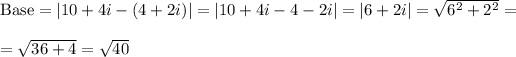
The middle point of the base is placed at point

`(4+2i+10+4i)/(2)=(6i+14)/(2)=7+3i`

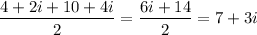
The length of the height is the distance between the points 5+9i and 7+3i

`\text{Height}=|5+9i-(7+3i)|=|5+9i-7-3i|=|-2+6i|=√((-2)^2+6^2)=\\ \\=√(4+36)=√(40)`

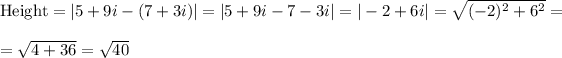
So, the area of the triangle is

`A=(1)/(2)\cdot \text{Base}\cdot \text{Height}=(√(40)\cdot √(40))/(2)`