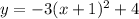Question

Use the information provided to write the equation of the parabola in vertex form.

y=-3x2 - 6x +1
A D=3(x+3)²+2
B. y = 3(x+1)+4
y=-3(x+3)² +2
D. y=-3(x+1)+4
Please help

Answer 1

Answer:
`y=-3(x+1)^2+4`

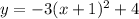
Explanation:

The vertex form of the equation of a parabola is:

`f(x) = a(x - h)^2 + k`

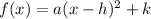
Where (h, k) is the vertex of the parabola.

To write
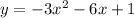`y=-3x^2 - 6x +1` in vertex form, you need to complete the square:

1. Move the 1 to the other side of the equation:

`y-1=-3x^2 - 6x`

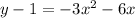
2. Since the leading coefficient must be 1, you need to factor out -3:

`y-1=-3(x^2 + 2x)`

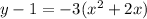
3. Divide the coefficient of the x-term inside the parentheses by 2 and square it:

`((2)/(2))^2=1`

4. Now add 1 inside the parethenses and -3(1) to the other side of the equation (because you factored out -3):

`y-1-3(1)=-3(x^2 + 2x+1)`

`y-4=-3(x^2 + 2x+1)`

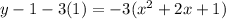
5. Convert the right side of the equation to a squared expression:

`y-4=-3(x+1)^2`

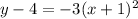
6. And finally, you must solve for "y":

`y=-3(x+1)^2+4`