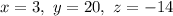Answer:
B.
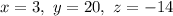
Explanation:
Consider the system of three equations:
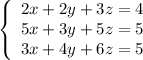
Multiply the first equation by 5, the second equation by 2 and subtract them:
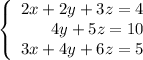
Multiply the first equation by 3, the second equation by 2 and subtract them:
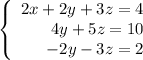
Multiply the third equation by 2 and add the second and the third equations:
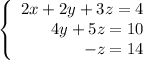
Fro mthe third equation
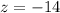
Substitute it into the second equation:
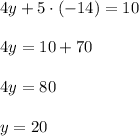
Substitute y=20 and z=-14 into the first equation:
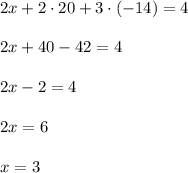
The solution is