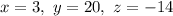Question

Solve the system of equations.
2x+2y+3z=4
5x+3y+5z=5
3x+4y+6z=5

Answer 1

B.
`x=3,\ y=20,\ z=-14`

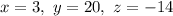
Explanation:

Consider the system of three equations:

`\left\{\begin{array}{l}2x+2y+3z=4\\5x+3y+5z=5\\3x+4y+6z=5\end{array}\right.`

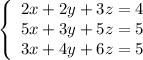
Multiply the first equation by 5, the second equation by 2 and subtract them:

`\left\{\begin{array}{r}2x+2y+3z=4\\4y+5z=10\\3x+4y+6z=5\end{array}\right.`

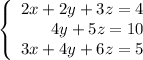
Multiply the first equation by 3, the second equation by 2 and subtract them:

`\left\{\begin{array}{r}2x+2y+3z=4\\4y+5z=10\\-2y-3z=2\end{array}\right.`

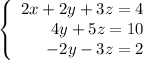
Multiply the third equation by 2 and add the second and the third equations:

`\left\{\begin{array}{r}2x+2y+3z=4\\4y+5z=10\\-z=14\end{array}\right.`

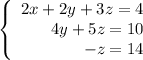
Fro mthe third equation

`z=-14`

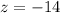
Substitute it into the second equation:

`4y+5\cdot (-14)=10\\ \\4y=10+70\\ \\ 4y=80\\ \\y=20`

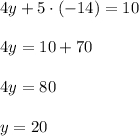
Substitute y=20 and z=-14 into the first equation:

`2x+2\cdot 20+3\cdot (-14)=4\\ \\2x+40-42=4\\ \\2x-2=4\\ \\2x=6\\ \\x=3`

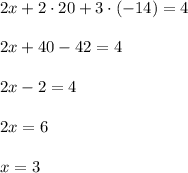
The solution is

`x=3,\ y=20,\ z=-14`