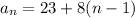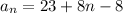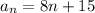Explicit formula
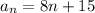
Recursive formula
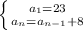
To solve this problem we have to use an arithmetic sequence. The cost of renting a kayak for 1 hour is $23, each additional hour is $8 more. So, the first element of the secuence will be 23 for one hour, then each addittional hour will be 23 + 8, making the secuence:
{23, 31, 39, 47, 55,.....,n}
Writing a recursive formula of the form
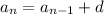 where
where
 is the nth term, n the number of terms, and d the common difference in the secuence.
is the nth term, n the number of terms, and d the common difference in the secuence.
The common difference of the secuence {23, 31, 39, 47, 55,.....,n}. So, the first term is
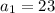 , and the common diffenece is d = 8 which is the difference between each term.
, and the common diffenece is d = 8 which is the difference between each term.
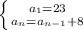
Writing a explicit formula of the form
 where where
where where
 is the nth term, n the number of terms,
is the nth term, n the number of terms,
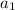 the first term of the secuence, and d the common difference in the secuence.
the first term of the secuence, and d the common difference in the secuence.
With
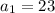 , and d = 8:
, and d = 8: