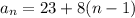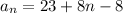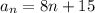Question

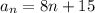
the cost of renting a kayak for one hour is $23. Each additional hour is 8$ more. Write an explicit formula and recursive formula to represent the situation.

Answer 1

X= 23+8y
X represents the total
23 represents the base price
8 represents the price per extra hour
Y represents how many hours extra

Answer 2

Explicit formula
`a_(n) =8n+15`

Recursive formula
`\left \{ {{a_(1) =23} \atop {a_(n)=a_(n-1)+8 }} \right.`

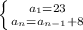
To solve this problem we have to use an arithmetic sequence. The cost of renting a kayak for 1 hour is $23, each additional hour is $8 more. So, the first element of the secuence will be 23 for one hour, then each addittional hour will be 23 + 8, making the secuence:

{23, 31, 39, 47, 55,.....,n}

Writing a recursive formula of the form
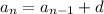`a_(n) =a_(n-1) +d` where
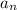`a_(n)` is the nth term, n the number of terms, and d the common difference in the secuence.

The common difference of the secuence {23, 31, 39, 47, 55,.....,n}. So, the first term is
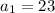`a_(1) =23`, and the common diffenece is d = 8 which is the difference between each term.

`\left \{ {{a_(1) =23} \atop {a_(n) =a_(n-1)+8 }} \right.`

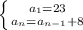
Writing a explicit formula of the form
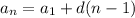`a_(n) =a_(1) +d(n-1)` where where
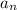`a_(n)` is the nth term, n the number of terms,
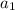`a_(1)` the first term of the secuence, and d the common difference in the secuence.

With
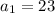`a_(1)=23`, and d = 8:

`a_(n) =23+8(n-1)`

`a_(n) =23+8n-8`

`a_(n) =8n+15`