Answer:
- Discontinuity at (-1,6)
- The zero is at (-7,0)
Explanation:
Given the function
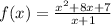 , you need to factor the numerator. Find two number whose sum be 8 and whose product be 7. These are 1 and 7, then:
, you need to factor the numerator. Find two number whose sum be 8 and whose product be 7. These are 1 and 7, then:
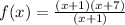
Then, the denominator is zero when

Therefore,
 does not belong to the Domain of the function. Then, (-1,6) is a discontinuity point.
does not belong to the Domain of the function. Then, (-1,6) is a discontinuity point.
Simplifying, you get:
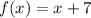
You can observe that a linear function is obtained.
This function is equal to zero when
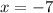 , therefore the zero of the function is at (-7,0).
, therefore the zero of the function is at (-7,0).