Question

Help Given the function f(x) = 4x + 10 and g(x), which function has a greater slope?

x g(x)
2 5
4 7
6 9
f(x) has a greater slope.
g(x) has a greater slope.
The slopes of f(x) and g(x) are the same.
The slope of g(x) is undefined.

Answer 1

`\bf f(x)=\stackrel{\stackrel{m}{\downarrow }}{4} x+10\qquad \impliedby \begin{array} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill`

`\bf \begin{array}{ccll} x&g(x)\\ \cline{1-2} 2&5\\4&7\\6&9 \end{array}~\hfill \begin{array}{llll} (\stackrel{x_1}{2}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{9}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{9-5}{6-2}\implies \cfrac{4}{4}\implies \stackrel{\stackrel{m}{\downarrow }}{1} \end{array}`

well, clearly 4 > 1.

Answer 2

f(x) has a greater slope.

Explanation:

The slope of a function in the form of y=Mx+C is represented by the letter M, so the slope in the function F(x) =4.

Now when you have a function but you only have a table to evaluate it, to calculate the slope you have the next formula:

`m=(y^(2)- y^(1))/(x^(2) -x^(1) )`

You just have to pick two points from the table to use in the formula, we´ll use (4,7) as our point 1 and

(6,9) as our point 2.

This means that:

`x^(1)=4`
`y^(1)=7`

`x^(2)=6`
`y^(2)=9`

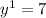
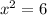
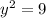
Now you just put it into the formula:

`m=(9-7)/(6-4)`

`m=(2)/(2)`

`m=1`

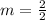
Now that you have both slopes, you can see that the slope of g(x)=1 and the slope of f(x)=4, and you can see that f(x) has a greater slope thatn g(x).