Answer:
f(x) has a greater slope.
Explanation:
The slope of a function in the form of y=Mx+C is represented by the letter M, so the slope in the function F(x) =4.
Now when you have a function but you only have a table to evaluate it, to calculate the slope you have the next formula:
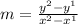
You just have to pick two points from the table to use in the formula, we´ll use (4,7) as our point 1 and
(6,9) as our point 2.
This means that:
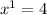
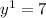
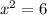
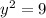
Now you just put it into the formula:
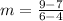
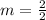
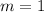
Now that you have both slopes, you can see that the slope of g(x)=1 and the slope of f(x)=4, and you can see that f(x) has a greater slope thatn g(x).