Question

An electric motor rotating a workshop grinding wheel at a rate of 1.31 ✕ 102 rev/min is switched off. Assume the wheel has a constant negative angular acceleration of magnitude 3.40 rad/s2. (a) How long does it take for the grinding wheel to stop? (b) Through how many radians has the wheel turned during the interval found in (a)?

Answer 1

(a) 4.03 s

The initial angular velocity of the wheel is

`\omega_i = 1.31 \cdot 10^2 (rev)/(min) \cdot (2\pi rad/rev)/(60 s/min)=13.7 rad/s`

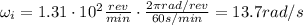
The angular acceleration of the wheel is

`\alpha = -3.40 rad/s^2`

negative since it is a deceleration.

The angular acceleration can be also written as

`\alpha = (\omega_f - \omega_i)/(t)`

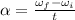
where

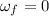`\omega_f = 0` is the final angular velocity (the wheel comes to a stop)

t is the time it takes for the wheel to stop

Solving for t, we find

`t=(\omega_f - \omega_i )/(\alpha)=(0-13.7 rad/s)/(-3.40 rad/s^2)=4.03 s`

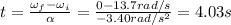
(b) 27.6 rad

The angular displacement of the wheel in angular accelerated motion is given by

`\theta= \omega_i t + (1)/(2)\alpha t^2`

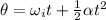
where we have

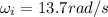`\omega_i=13.7 rad/s` is the initial angular velocity

`\alpha = -3.40 rad/s^2` is the angular acceleration

t = 4.03 s is the total time of the motion

Substituting numbers, we find

`\theta= (13.7 rad/s)(4.03 s) + (1)/(2)(-3.40 rad/s^2)(4.03 s)^2=27.6 rad`