Answer:
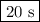
Explanation:
The standard form of a quadratic function is
y = ax² + bx + c
Your function is
h(t) = -16t²+ 640t
a = -16; b = 640; c = 0
a is negative, so you have a downward-opening parabola.
The vertex form of a parabola is
y = a(x - h)² + k
where (h, k) is the vertex of the parabola.
h = -b/(2a) and k = f(h)
Your parabola opens downward, so the vertex is a maximum.
Calculate h
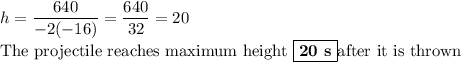
The figure below shows the graph of h(t).