Question

If two polynomial equations have real solutions, then will the equation that is the result of adding, subtracting, or multiplying the two polynomial equations also have real solutions?

Answer 1

No.

Explanation:

No, one easy way to see it is with quadratic formulas. There exists quadratic polynomials with no real solutions, then if you add, subtract or multiply two polynomials and obtain a quadratic formula, possibly this polynomial won't have real solutions.

I am going to give one counterexample:

We have the two polynomials
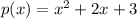`p(x) = x^2+2x+3` and
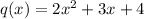`q(x)= 2x^2+3x+4`, then is we subtract q(x)-p(x) we obtain

`2x^2+3x+4-(x^2+2x+3) = 2x^2+3x+4-x^2-2x-3 = x^2+x+1.`

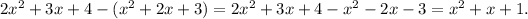
The resulting polynomial is a quadratic polynomial of the form
`ax^2+bx+c` with a=1, b=1 and c=1. This polynomial has no real solutions, you can check it with the discriminating
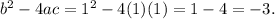`b^2-4ac = 1^2-4(1)(1) = 1-4 = -3.` As the discriminating is negative, the polynomial has no real solutions.

Answer 2

No, there are polynomials that have real solutions but when combined would be possible to have no real solutions.