Answer:
The fourth term is
 .
.
Explanation:
The given binomial expression is
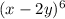 .
.
When we compare this to the general binomial expression,
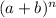 , we have
, we have
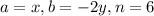 .
.
The specific term in a binomial expansion with an integral index is given by:
 .
.
To find the fourth term, we set
 . This implies that;
. This implies that;
 .
.
We now substitute the values into the formula to obtain:
 .
.
We simplify to get:
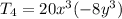 .
.
 .
.
Therefore the fourth term is
 .
.