Answer:
Option C
Explanation:
Two triangles are similar if they have at least 2 equal angles
Note that the HEF triangle has angles of 90 °, 60 ° and 30 °
Note that the EGF triangle has angles of 90 ° and 30 ° so the third angle must be 60 °
Then HEF and EGF are similar triangles.
By definition for similar triangles it is satisfied that if they have sides of length a, b, c and a ', b' c' then
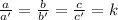
Where the constant k is known as "scale factor"
In this case
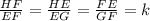
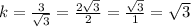
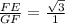
or
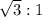
The answer is Option C