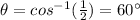Answer:
D 60°
Step-by-step explanation:
Using trigonometry:
- The new speed (v/2) of the particle corresponds to the hypothenuse
- The component of v/4 represents the side adjacent to the angle that we want fo find,

So we can write:

So we find the angle