Question

A small bouncy ball with a momentum of 8 kg∙m/s to the left approaches head-on a large door at rest. The ball bounces straight back with a momentum of 6 kg∙m/s. What is the change in the momentum of the ball? What is the impulse exerted on the ball? What is the impulse exerted on the door?

Answer 1

-14 kg m/s

Step-by-step explanation:

Taking the direction "to the left" as positive direction, the initial momentum of the ball is

p1 = +8 kg m/s

while the final momentum is

p2 = -6 kg m/s

so the change in momentum is

`\Delta p = p_2 - p_1 = -6kg m/s - (8 kg m/s) = -14 kg m/s`

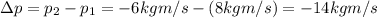
According to the impulse theorem, the impulse exerted on the ball is equal to the change in momentum of the ball, so:

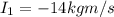`I_1 = -14 kg m/s` (which means 14 kg m/s to the right)

While the impulse that the ball exerted on the ball is equal and opposite in direction, so:

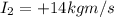`I_2 = + 14 kg m/s` (which means towards the left)