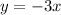Answer:
y varies directly with x

The equation is:
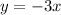
Explanation:
We can say that and it varies directly with x if it is fulfilled that

Where k is a constant known as the constant of variation.
So
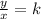
This means that if y varies with x then the division of y between x should always be equal to a constant value k.
We must test this for the values shown in the table
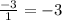
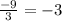

The quotient of
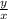 is always equal to
is always equal to
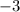 . Then
. Then
 and the variation of y with x is direct
and the variation of y with x is direct
The equation is: