Answer with explanation:
Formula to find the margin of error :
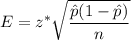 , where n= sample size ,
, where n= sample size ,
 is the sample proportion and z*= critical z-value.
is the sample proportion and z*= critical z-value.
Let p be the proportion of 19-year-olds had a driver’s license.
A) As per given , In 1983
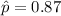
n= 1200
Critical value for 95% confidence level is 1.96 (By z-table)
So ,Margin of error :
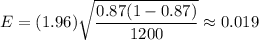
Interval :
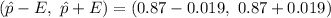
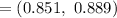
B) In 2008 ,
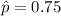
Margin of error :
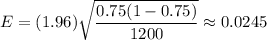
Interval :

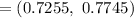
c. The margin of error is not the same in parts (a) and (b) because the sample proportion of 19-year-olds had a driver’s license are not same in both parts.