Question

. Need help !!! on 2 math questions

The height in feet of a ball dropped from a 150 ft. Building is given by h(t) = –16t2 + 150, where t is the time in seconds after the ball is dropped. Find h(2) and interpret its meaning. Round your answer to the nearest hundredth.

A. h(2) = 86.00 means that after 2 seconds, the height of the ball is 86.00 ft.


B. h(2) = 3.04 means that after 2 seconds, the height of the ball has dropped by 3.04 ft.


C. h(2) = 3.04 means that after 2 seconds, the height of the ball is 3.04 ft.


D. h(2) = 86.00 means that after 2 seconds, the height of the ball has dropped by 86.00 ft.


15. The perimeter of a triangle is 69 cm. The measure of the shortest side is 5 cm less than the middle side. The measure of the longest side is 5 cm less than the sum of the other two sides. Find the lengths of the sides.


A. 16 cm; 21 cm; 32 cm


B. 15 cm; 21 cm; 33 cm


C. 15 cm; 22 cm; 32 cm


D. 17 cm; 21 cm; 31 cm

Answer 1

Part 1) Option A. h(2) = 86.00 means that after 2 seconds, the height of the ball is 86.00 ft.

Part 2) Option A. 16 cm; 21 cm; 32 cm

Explanation:

Part 1)

we have

`h(t)=-16t^(2)+150`

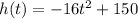
where

t ----> is the time in seconds after the ball is dropped

h(t) ----> he height in feet of a ball dropped from a 150 ft

Find h(2)

That means ----> Is the height of the ball 2 seconds after the ball is dropped

Substitute the value of t=2 sec in the equation

`h(2)=-16(2)^(2)+150=86\ ft`

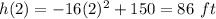
therefore

After 2 seconds, the height of the ball is 86.00 ft.

Part 2) The perimeter of a triangle is 69 cm. The measure of the shortest side is 5 cm less than the middle side. The measure of the longest side is 5 cm less than the sum of the other two sides. Find the lengths of the sides

Let

x----> the measure of the shortest side

y ----> the measure of the middle side

z-----> the measure of the longest side

we know that

The perimeter of the triangle is equal to

P=x+y+z

P=69 cm

so

69=x+y+z -----> equation A

x=y-5 ----> equation B

z=(x+y)-5 ----> equation C

substitute equation B in equation C

z=(y-5+y)-5

z=2y-10 -----> equation D

substitute equation B and equation D in equation A and solve for y

69=(y-5)+y+2y-10

69=4y-15

4y=69+15

4y=84

y=21 cm

Find the value of x

x=21-5=16 cm

Find the value of z

z=2(21)-10=32 cm

The lengths of the sides are 16 cm, 21 cm and 32 cm