Question

What is the equation for the hyperbola shown? PLEASE HELP

Answer 1

`((y^2)/(25)-(x^2)/(64)=1`

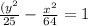
Explanation:

We have been given an image of a hyperbola. We are asked to write an equation for our given hyperbola.

We can see that our given hyperbola is a vertical hyperbola as it opens upwards and downwards.

We know that equation of a vertical hyperbola is in form
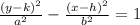`((y-k)^2)/(a^2)-((x-h)^2)/(b^2)=1`, where,
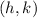`(h,k)` represents center of hyperbola.

'a' is vertex of hyperbola and 'b' is co-vertex.

We can see that center of parabola is at origin (0,0).

We can see that vertex of parabola is at point
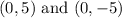`(0,5)\text{ and }(0,-5)`, so value of a is 5.

We can see that co-vertex of parabola is at point
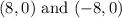`(8,0)\text{ and }(-8,0)`, so value of b is 8.

`((y-0)^2)/(5^2)-((x-0)^2)/(8^2)=1`

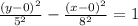
Therefore, our required equation would be
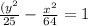`((y^2)/(25)-(x^2)/(64)=1`.

Answer 2

`\frac{ {y}^(2) }{ 25} - \frac{ {x}^(2) }{ 64} = 1`

EXPLANATION

The given hyperbola has a vertical transverse axis and its center is at the origin.

The standard equation of such a parabola is:

`\frac{ {y}^(2) }{ {a}^(2) } - \frac{ {x}^(2) }{ {b}^(2) } = 1`

Where 2a=10 is the length of the transverse axis and 2b=16 is the length of the conjugate axis.

This implies that

`a = 5 \: \: and \: \: b = 8`

Hence the required equation of the hyperbola is:

`\frac{ {y}^(2) }{ {5}^(2) } - \frac{ {x}^(2) }{ {8}^(2) } = 1`

This simplifies to,

`\frac{ {y}^(2) }{ 25} - \frac{ {x}^(2) }{ 64} = 1`