Question

What is the average rate of change for f(x) = 2 ^ x - 12 over the interval 4 <= x <= 8

Answer 1

The everage rate of change over the interal 4 ≤ x ≤ 8 will be: 60

Explanation:

Given the function

`f\left(x\right)\:=\:2^x-\:12\:\:\:`

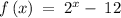
Interval : 4 ≤ x ≤ 8

or

Interval = [4, 8]

so

at x₁ = 4, f(x₁) = 2ˣ - 12 = 2⁴ - 12 = 16-12 = 4

at x₂ = 8, f(x₂) = 2ˣ - 12 = 2⁸ - 12 = 256 - 12 = 244

Using the formula to determine the average rate of change over the interval 4 ≤ x ≤ 8 wil be:

Average rate = [f(x₂) - f(x₁)] / [ x₂ - x₁]

= [244 - 4] / [8-4]

= 240 / 4

= 60

Therefore, the everage rate of change over the interal 4 ≤ x ≤ 8 will be: 60