Answer:
The everage rate of change over the interal 4 ≤ x ≤ 8 will be: 60
Explanation:
Given the function
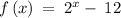
Interval : 4 ≤ x ≤ 8
or
Interval = [4, 8]
so
at x₁ = 4, f(x₁) = 2ˣ - 12 = 2⁴ - 12 = 16-12 = 4
at x₂ = 8, f(x₂) = 2ˣ - 12 = 2⁸ - 12 = 256 - 12 = 244
Using the formula to determine the average rate of change over the interval 4 ≤ x ≤ 8 wil be:
Average rate = [f(x₂) - f(x₁)] / [ x₂ - x₁]
= [244 - 4] / [8-4]
= 240 / 4
= 60
Therefore, the everage rate of change over the interal 4 ≤ x ≤ 8 will be: 60