Answer:
Angle = Ф =
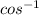 (0) = 0
(0) = 0
Hence, it is proved that angle between position vector r and acceleration vector a = 0 and is it never changes.
Explanation:
Given vector r(t) =
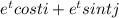
As we know that,
velocity vector = v =

Implies that
velocity vector =
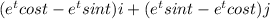
As acceleration is velocity over time so:
acceleration vector = a =
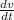
Implies that
vector a =
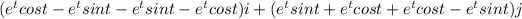
vector a =
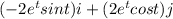
Now scalar product of position vector r and acceleration vector a:
r. a =
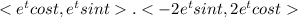
r.a =
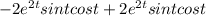
r.a = 0
Now, for angle between position vector r and acceleration vector a is given by:
cosФ =
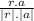 =
=
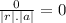
Ф =
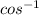 (0) = 0
(0) = 0
Hence, it is proved that angle between position vector r and acceleration vector a = 0 and is it never changes.