Question

Suppose r(t) = (et cos t)i + (et sin t)j. Show that the angle between r and a never changes. What is the angle?

Answer 1

Angle = Ф =
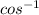`cos^(-1)`(0) = 0

Hence, it is proved that angle between position vector r and acceleration vector a = 0 and is it never changes.

Explanation:

Given vector r(t) =
`e^(t)cost i + e^(t)sint j`

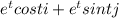
As we know that,

velocity vector = v =
`(dr)/(dt)`

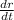
Implies that

velocity vector =
`(e^(t) cost - e^(t) sint)i + (e^(t) sint - e^(t)cost )j`

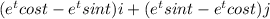
As acceleration is velocity over time so:

acceleration vector = a =
`(dv)/(dt)`

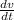
Implies that

vector a =

`(e^(t)cost - e^(t)sint - e^(t)sint - e^(t)cost )i + ( e^(t)sint + e^(t)cost + e^(t)cost - e^(t)sint )j`

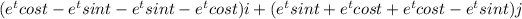
vector a =
`(-2e^(t)sint) i + ( 2e^(t)cost)j`

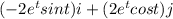
Now scalar product of position vector r and acceleration vector a:

r. a =
`<e^(t)cost, e^(t)sint> . <-2e^(t)sint, 2e^(t)cost>\\`

r.a =
`-2e^(2t)sintcost + 2e^(2t)sintcost`

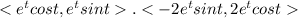
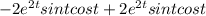
r.a = 0

Now, for angle between position vector r and acceleration vector a is given by:

cosФ =
`(r.a)/(|r|.|a|)` =
`(0)/(|r|.|a|) = 0`

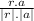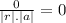
Ф =
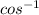`cos^(-1)`(0) = 0

Hence, it is proved that angle between position vector r and acceleration vector a = 0 and is it never changes.