Answer:
If the function is
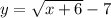 , the domain are all values of x greater than or equal to -6
, the domain are all values of x greater than or equal to -6
If the function is
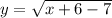 , the domain are all values of x greater than or equal to 1
, the domain are all values of x greater than or equal to 1
Explanation:
First case
we have
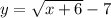
we know that
The radicand of the function must be greater than or equal to zero
so
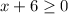
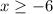
the solution is the interval---------> [-6,∞)
therefore
The domain are all values of x greater than or equal to -6
Second case
we have
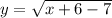
so
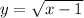
we know that
The radicand of the function must be greater than or equal to zero
so

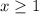
the solution is the interval---------> [1,∞)
therefore
The domain are all values of x greater than or equal 1