Answer:
C. Center (3,-2) and radius 3
Explanation:
The given circle has equation:
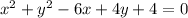
We rearrange to get:
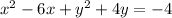
We add the square of half the coefficients of the linear terms to both sides of the equation:

We factor the perfect squares and simplify to get;
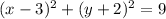
We can rewrite as;
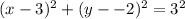
Comparing this to the standard equation of the circle;
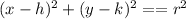
We have (3,-2) and the center and r=3 as the radius.