Question

What is the approximate length of minor arc XZ? Round to the nearest tenth of a meter. 1.8 meters 3.7 meters 15.2 meters 18.8 meters

Answer 1

B!!! 3.7

Explanation:

ON EDG2020

Answer 2

Here is the complete question.

`Consider \ circle \ Y \ with \ radius \ 3 m \ and \ central \ angle \ XYZ \ measuring \ 70°. \\ \\ What \ is \ the \ approximate \ length \ of \ minor \ arc \ XZ?\\ \\ Round \ to \ the \ nearest \ tenth \ of \ a \ meter. \\ 1.8 meters \\ 3.7 \ meters \\ 15.2\ meters \\ 18.8 \ meters`

Answer:

3.7 meters

Explanation:

From the given information:

The radius is 3m

The central angle XYZ = 70°

To calculate the circumference of the circle:

C = 2 π r

C = 2 × 3.142 × 3

C = 18.852 m

Let's recall that:

The circumference length define a central angle of 360°

The approximate length of minor arc XZ can be determined as follow:

Suppose the ≅ length of minor arc XZ = Y

By applying proportion;

`(18.852)/(360) = (Y)/(70)`

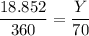
Y(360) = 18.852 × 70

Y = 1319.64/360

Y = 3.66

Y ≅ 3.7 m