Here is the complete question.

Answer:
3.7 meters
Explanation:
From the given information:
The radius is 3m
The central angle XYZ = 70°
To calculate the circumference of the circle:
C = 2 π r
C = 2 × 3.142 × 3
C = 18.852 m
Let's recall that:
The circumference length define a central angle of 360°
The approximate length of minor arc XZ can be determined as follow:
Suppose the ≅ length of minor arc XZ = Y
By applying proportion;
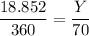
Y(360) = 18.852 × 70
Y = 1319.64/360
Y = 3.66
Y ≅ 3.7 m