Question

Which complex number has a distance of the root of 17 from the origin on the complex plane?

2 + 15i
17 + i
20 – 3i
4 – i

Answer 1

4 – i

Explanation:

First, we need to know that a complex number, which has a real part and an imaginary part, it's like a vector, where the horizontal coordinate is the real part, and the vertical coordinate is the imaginary part.

So, to find the distances we applied the conventional definition:

`d=\sqrt{r^(2)+i^(2) }`

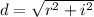
Where
`r` refers to the real part and
`i` refers to the imaginary part.

So, we test each answer and see which one gives us the root of 17.

Option 1.

`d=\sqrt{2^(2)+15^(2) }=√(4+225)=√(229)`

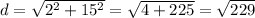
Option 2.

`d=\sqrt{17^(2)+1^(2) }=√(290)`

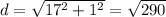
Option 3.

`d=\sqrt{20^(2)+(-3)^(2) }=√(409)`

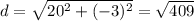
Option 4.

`d=\sqrt{4^(2)+(-1)^(2) }=√(17)`

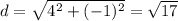
Therefore, the right answer is the last one, because the distance is the squared root of 17.

Answer 2

4 -i

Explanation:

For your condition to be met, neither the real part nor the imaginary part can exceed √17 in magnitude. That excludes the first three answer choices.

The magnitude of 4-i is ...

√(4^2 +(-1)^2) = √17.