Question

What is the solution to sqrt 17-x=x+3? Show your work.

Answer 1

`x=1`

Explanation:

Remember:

`(\sqrt[n]{a})^n=a\\\\(a+b)=a^2+2ab+b^2`

Given the equation
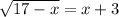`√(17-x)=x+3`, you need to solve for the variable "x" to find its value.

You need to square both sides of the equation:

`(√(17-x))^2=(x+3)^2`

`17-x=(x+3)^2`

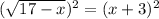
Simplifying, you get:

`17-x=x^2+2(x)(3)+3^2\\\\17-x=x^2+6x+9\\\\x^2+6x+9+x-17=0\\\\x^2+7x-8=0`

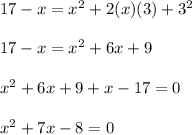
Factor the quadratic equation. Find two numbers whose sum be 7 and whose product be -8. These are: -1 and 8:

`(x-1)(x+8)=0`

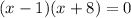
Then:

`x_1=1\\x_2=-8`

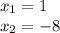
Let's check if the first solution is correct:

`√(17-(1))=(1)+3`

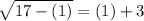
`4=4` (It checks)

Let's check if the second solution is correct:

`√(17-(-8))=(-8)+3`

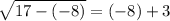
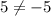`5\\eq-5` (It does not checks)

Therefore, the solution is:

`x=1`