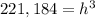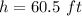Question

The water tank in the diagram is in the shape of an inverted right circular cone. The radius of its base is 16 feet, and its height is 96 feet. What is the height, in feet, of the water in the tank if the amount of water is 25% of the tank’s capacity?

Answer 1

6433.98 ft

Explanation:

In order to find what 25% of the tank's capacity is, we know to know the full capacity of the tank then take 25% of that. The volume formula for a right circular cone is

`V=(1)/(3)\pi r^2h`

We have all the values we need for that:

`V=(1)/(3)\pi (16)^2(96)`

This gives us a volume of 25735.93 cubic feet total.

25% of that:

.25 × 25735.93 = 6433.98 ft

Answer 2

The height of the water is
`60.5\ ft`

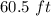
Explanation:

step 1

Find the volume of the tank

The volume of the inverted right circular cone is equal to

`V=(1)/(3)\pi r^(2) h`

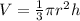
we have

`r=16\ ft`

`h=96\ ft`

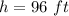
substitute

`V=(1)/(3)\pi (16)^(2) (96)`

`V=8,192\pi\ ft^(3)`

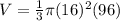
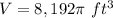
step 2

Find the 25% of the tank’s capacity

`V=(0.25)*8,192\pi=2,048\pi\ ft^(3)`

step 3

Find the height, of the water in the tank

Let

h ----> the height of the water

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional

`(R)/(H)=(r)/(h)`

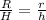
substitute

`(16)/(96)=(r)/(h)\\ \\r= (h)/(6)`

where

r is the radius of the smaller cone of the figure

h is the height of the smaller cone of the figure

R is the radius of the circular base of tank

H is the height of the tank

we have

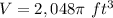`V=2,048\pi\ ft^(3)` -----> volume of the smaller cone

substitute

`2,048\pi=(1)/(3)\pi ((h)/(6))^(2)h`

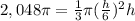
Simplify

`221,184=h^(3)`

`h=60.5\ ft`