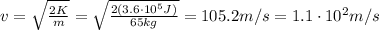Question

A) How many joules of energy does a 100-watt light bulb use per hour? Express your answer using two significant figures.

B) How fast would a 65 kg person have to run to have that amount of energy? Express your answer using two significant figures.

Answer 1

A)
`3.6\cdot 10^5 J`

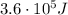
The power used by an object is defined as

`P=(E)/(t)`

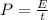
where

E is the energy used

t is the time elapsed

In this problem, we have

P = 100 W is the power of the light bulb

t = 1 h = 3600 s is the time elapsed

Solving for E, we find the amount of energy used by the light bulb:

`E=Pt = (100 W)(3600 s)=3.6\cdot 10^5 J`

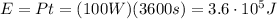
B)
`1.1 \cdot 10^2 m/s`

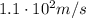
The kinetic energy of an object is given by

`K=(1)/(2)mv^2`

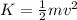
where

m is the mass

v is the speed of the object

In this problem, we have a man of mass

m = 65 kg

we want its kinetic energy to be

`E=3.6\cdot 10^5 J`

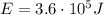
Therefore, we can calculate its speed from the previous formula:

`v=\sqrt{(2K)/(m)}=\sqrt{(2(3.6\cdot 10^5 J))/(65 kg)}=105.2 m/s = 1.1 \cdot 10^2 m/s`